【朝活】【数学】フェルマーの最終定理（8/20更新）

Fermat's Last Theorem（フェルマーの最終定理）
8/17のグーグルのロゴは、「フェルマーの最終定理」についてでした。
（8/17は、フェルマーの生誕日だったからのようです。）

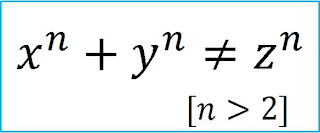googleホリデーロゴ（8/17）のイメージ

「フェルマーの最終定理」を英語でどう書くかをwikipediaで調べてみました。

◆Fermat's Last Theorem
Fermat's Last Theorem states that
no three positive integers x, y, and z can satisfy
the equation
x^n + y^n = z^n
for any integer value of n greater than 2.

◆フェルマーの最終定理
nが2より大きい自然数のとき、方程式
x^n + y^n = z^n
をみたす自然数の組x、y、zは存在しない。

■
「フェルマーの最終定理（大定理、予想）」は、もともとは、1630年頃、フランス人フェルマーが、自身が読んでいた本の欄外に書いたものだそうです。
（8/17のグーグルのロゴをみるとわかるように、）定理（予想）自体は非常にシンプルでした。
ところが、定理（予想）を証明するのに、1995年にアンドリュー・ワイルズが証明するまで、約360年間の月日を必要としました。


◆三平方（ピタゴラス）の定理（Pythagorean theorem）
フェルマーの最終定理の方程式は、
nが2であれば、解を持ちます。
（たしか）中学校で習う「三平方の定理」です！

三平方（ピタゴラス）の定理

◆Pythagorean theorem
x^2 + y^2 = z^2
where z represents the length of the hypotenuse, and x and y represent the lengths of the other two sides

直角三角形の斜辺（hypotenuse）の長さを zとし、その他の辺の長さを x, y とすれば、
x^2 + y^2 = z^2

例えば、
x^2 + y^2 = z^2
をみたすxとyとzの組として、(3,4,5)や(5,12,13)が存在します。

【例】
3×3 + 4×4 = 5×5
5×5＋12×12＝13×13


　

三平方の定理例1

 　

三平方の定理例2

      

■私が勝手に感じた魅力
「三平方の定理」からのイメージ（根拠ない・・・）では、
nが2より大きい整数でも、方程式をみたすxとyとzの組はありそうなものです。
ところが、フェルマーの最終定理は、
「nが2より大きい整数なら存在しない！」
と主張するのです。
とても興味深く思いました。

もうひとつは、足立さん（1995）の本に書いてあったことです。
1994年の初めでは、
「nが400万以下であれば定理は正しい」
ということがわかっていたのですが、「nが2より大きなすべての整数nについて」はわかっていませんでした。
「nが400万以下で成り立つならおそらく大丈夫じゃないか」
となんとなく思いがちですが、「すべての整数」についてでなければ証明にならないのです。
「無限を扱う」大変さと面白さを同時に感じました。

＜参考文献＞
wikipedia
http://en.wikipedia.org/wiki/Fermat%27s_Last_Theorem

足立恒雄 1995 フェルマーの大定理が解けた！ 講談社